さて、前回プロジェクトのビットとサンプリング周波数についての話にちょっと触れましたが、このビットとかサンプリング周波数というものについて、よく聞くけど何のことだかよくわかっていない、という人も多いのではないでしょうか。それもそのはず、この辺の知識はプロのレコーディングエンジニアさんでもわりと知ったかぶりだったりするのです。
そういうわけで、僕なりにわかりやすい説明で解説してみたいと思います。これを機会に正しい知識を見につけましょう!
アナログとかデジタルって何?
アナログとかデジタルとか良く聞くけど、そもそもどういう意味なんでしょうか?
アナログとは人間などの生物が五感で感知している情報そのものです。デジタルとはコンピュータに理解してもらうためにアナログを変換した情報です。
たとえば、音は波です。波というのはこんな感じです。
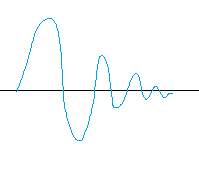
今これを見るとなめらかに見えますが、拡大して見るとこんな感じです。
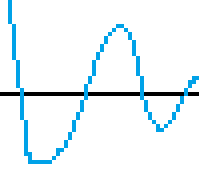
この一見なめらかに見えるけど実はギザギザなのがデジタルなのです。インターネットでとびかう情報はすべてデジタルなので、ここでアナログの波をお見せすることはできません。…というのはウソで、人間はアナログしか感知できないので、実はみなさんはアナログでこのギザギザを見ています。液晶モニタの画面はアナログです。「え?うちの液晶はデジタルだけど?」違います。パソコンとモニターの接続はデジタルでも、液晶モニタの画面自体はアナログなのです。同じような勘違いにデジカメのセンサ(CMOSやCCDなど)やスキャナやプリンタなどもあります。それらはすべてアナログの装置なのです。
これは本気出すとかなり長い話になってしまうので、ここでは音に限っての話にしましょう。
※以後、デジタルオーディオの中でも一番普及しているPCMオーディオに限定して話を進めます。DSDなどの場合には仕組みが違いますが、DTMの知識としては現在のところあまり重要ではないので割愛します。
みなさんが音楽を聴いてる時に何がデジタルで何がアナログでしょうか? 今はほとんど見かけないカセットテープやレコードはアナログです。じゃあCDは?iPodは?これらもアナログです。「え?デジタルじゃねーの?」と思うでしょう。はい。確かに記録はデジタルでされていますが、聴く時にはアナログです。ハイレゾ音源?それだってアナログでしか聴けません。人間にはアナログしか感知できないのです。
ためしに音楽が作られて聴かれるまでを追ってみましょう。まず、ミュージシャンが歌ったり演奏したりします。それをマイクで録音します。録音したものをパソコンで編集してMP3にしてネットに公開します。それを誰かがダウンロードして再生して聴きます。
この流れの中で、最初の歌声は人間が発するものです。つまりここはアナログでしかありえません。アナログを取り込むためのマイクもアナログです。マイクがささっている機器(レコーダーやミキサーなど)の端子まではアナログで、一般的にはここでデジタルに変換されます(A/D変換)。
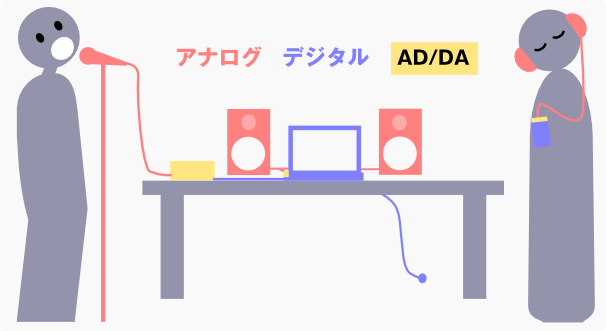
デジタルになったものはパソコンやインターネットの中で利用できるのでデジタルのままあちこちを移動し、最終的にリスナーのパソコンやスマホ、プレーヤーなどに届きます。この間はずっとデジタルです。
プレイヤーやパソコンで再生すると、その出口の直前でアナログに変換され(D/A変換)、ヘッドフォンまたはスピーカーに送られます。人間の耳で聞くものなので、ヘッドフォンやスピーカはアナログでなければなりません。
このように人間が使うものである以上、どんなに技術が進化してもどんなにデジタル化しても最初の入口と最後の出口はアナログなのです。
では、入口も出口もアナログなのにどうして途中でデジタルにするのかというと、理由は2つです。1つはコンピュータのデータとして保存できるのはデジタルだけだから。もう1つはアナログは情報量が多すぎてコピーしたり移動したりできないからです。アナログはコピーしたり移動したりしようとするとかならず劣化します。だから情報を間引いてコピーしやすくするのです。このコピーしやすくするために間引いた情報がデジタルなのです。よく「デジタルは劣化しない」といいますが、これは「アナログは劣化する、デジタルは劣化しない、だからデジタルの方が良い」という意味で理解されていることが多いのですが、実際には「アナログからデジタルにする時にあらかじめ劣化させておけば、その後デジタルのままコピーする際にはそれ以上劣化することがない」という意味です。アナログの場合にはコピーするたびに少しずつ劣化しますが、デジタルの場合は最初にガツンと劣化しその後は劣化しない、ということです。ちなみに、ここでいう「劣化」とはいわゆるmp3などの圧縮の話ではありませんので注意してください。圧縮の話については機会があれば後日書きたいと思います。
前置きが長くなりましたが、今回はそのデジタルオーディオのフォーマットについての解説です。「CDは 16Bit 44.1kHz である」とか、「録音は 24Bit 96kHzでお願いします」とか、「うちのDAWは内部演算 32Bit Float だよ」というような使われ方をする「ビット深度(Bit)」と「サンプリング周波数(Hz)」について解説します。
ビットって何?
デジタルオーディオで言うビット(bit)とは、音声波形の音量に対する分解能のことです。「うちのパソコンはWindows 7 の 64Bitだよー」のBitはまた意味が違いますので今は忘れてください(後述します)。
ギザギザしたデジタル音声の波形をもう一度見てください。
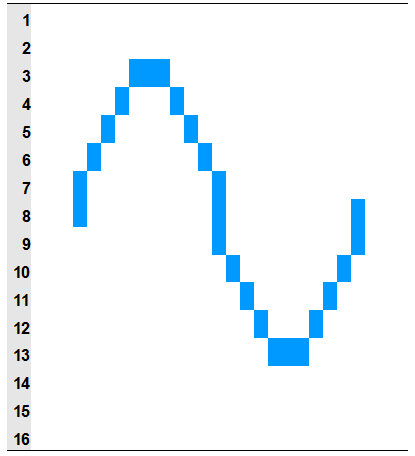
わかりやすいようにマス目を書きます。
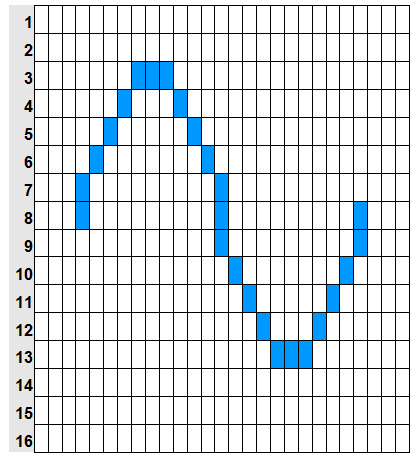
これ、ギザギザしてるけど、このマス目を分割してもっと細かくしたらなめらかになるんじゃね?
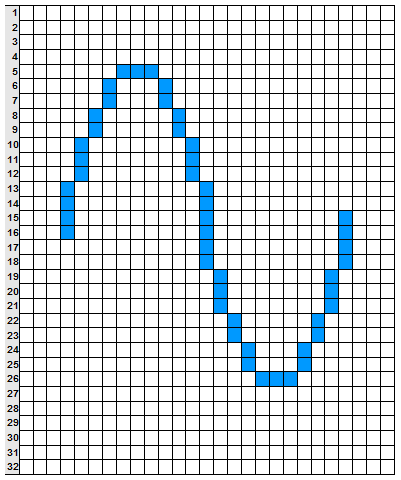
ということで、縦のマス目を細かくしてみました。横はそのままに縦だけ細かく分割してみました。この縦のマス目の細かさを示す数値がビット深度(Bit)です。Bit数が大きいほど細かくなります。たとえば16Bitと32Bitだと32Bitの方が細かく分割されています。では16Bitと32Bitでは、どのくらい細かさが違うのでしょう? 2倍?いえ、違います。
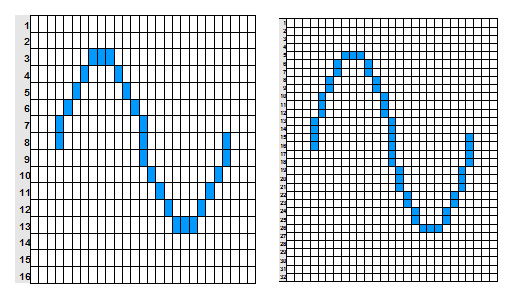
上の図を見てください。4Bitは波形を16分割、5Bitは波形を32分割しています。Bitの数値は「2のn乗」のnを指します。4Bitは2の4乗で16、5Bitは2の5乗で32です。ですので、1Bit増えるごとに2倍になります。ということは16Bitと32Bitでは細かさが何倍違うのでしょうか? 2の16乗は65,536、2の32乗は4,294,967,296ですので、4,294,967,296/65,536=65,536、ということで65536倍違う、ということになります。ちなみに実際には上図のような4Bitや5Bitではまともな音にはなりません。音楽として使えるのは最低でも8Bit、現実的には12Bit以上となります。CDやMP3は16Bitです。
※以後、図を使っての解説がつづきますが、これらはすべて説明上わかりやすいようにあえて簡略化した概念図です。特にゼロのあたりに誤魔化しがありますので気付いた方はフフっと見過してあげてください(笑)
サンプリング周波数って何?
先ほどの図では縦の分割を変えてみました。

でもこれ、横の分割も細かくしたらもっとなめらかになるんじゃね?
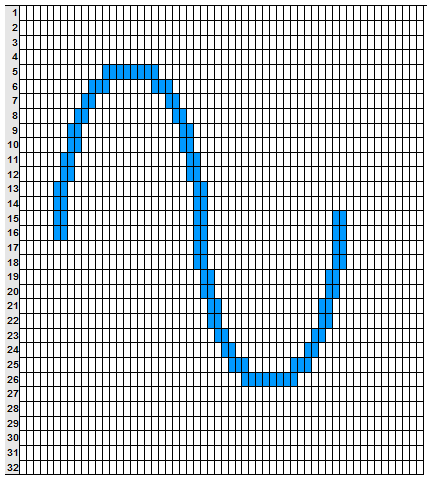
とやってたらこうなります。この横の分割の細かさを示す数値がサンプリング周波数(Hz)です。一秒間に何分割するかを示します。44.1kHzは1秒間を44100分割しています。なのでBitと違って数値が2倍になると細かさも単純2倍です。
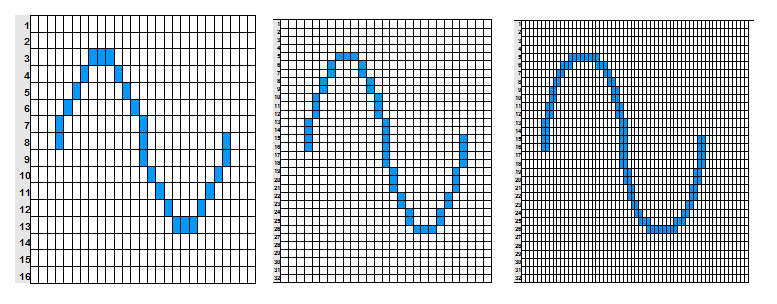
このように波形を表示した状態だと、ビット深度(Bit)とサンプリング周波数(Hz)は単純に縦の細かさと横の細かさというだけに見えますが、音の性質上はビット深度(Bit)は波形の振幅つまり音の大きさに影響し、サンプリング周波数(Hz)は波形の周期つまり音の高さに影響します。このことがどういうBit数とサンプリング周波数を使用するのかに影響します。これについてはもう少し後に解説します。
違うビットや違うサンプリング周波数の音をミックスする(混ぜる/重ねる)場合の注意点
アナログであれデジタルであれ、音楽を作る上では複数の音を混ぜる(ミックス)作業は必須です。デジタルオーディオ上では、ミックスというのは単純な足し算で、例えば2つの波形をミックスすると下の図のようになります。
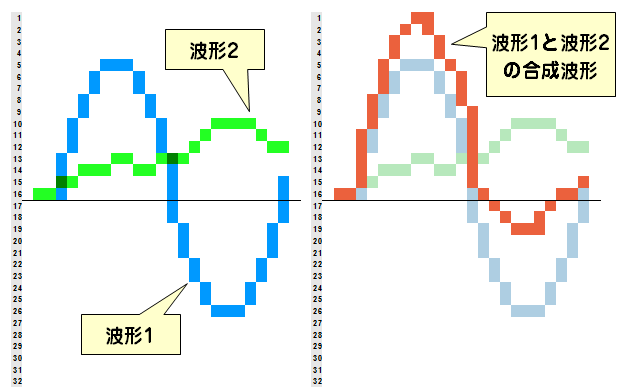
この時、ビットの違うオーディオファイル同士を重ねても特に問題はありません。たとえば4Bitの音と5Bitの音を同じレベルで単純にミックスしてみるとこんな感じです。
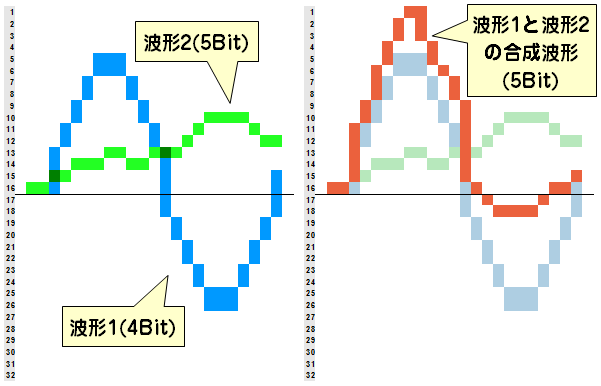
このように、ミックスされた音の解像度は5Bitになります。
このように違うビット深度(Bit)のデジタル音同士は混ぜる(重ねる/ミックスする)ことができますが、違うサンプリング周波数(Hz)のデジタル音同士を混ぜることは原理上はできません。なぜなのかというと、Bitが違うもの同士は片方がもう一方の整数倍になっているため、大きいビット深度の音が小さいビット深度の音を完璧に表現できますが、サンプリング周波数(Hz)が違うもの同士は(たまたま整数倍になっていることもありますが)一方が他方を完璧に再現することはできないからです。このため原理上は直接混ぜることはできません。
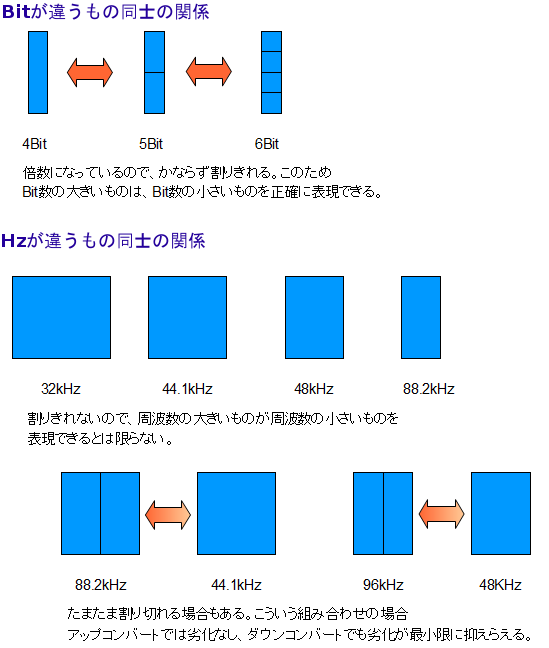
ただし、どちらかのサンプリング周波数を変更(コンバート)して同じサンプリング周波数に揃えれば混ぜることができます。「じゃあ問題ないじゃん」と思うかもしれませんが、サンプリング周波数(Hz)のコンバートでは音質が劣化します。ビット深度(Bit)は下げる場合だけ劣化するのですが、サンプリング周波数(Hz)の場合には上げる場合でも劣化します(整数倍の場合を除く)。
最近のDAWはオーディオファイルをインポートする際に音声ファイルを自動的にプロジェクトのサンプリング周波数にコンバートしてくれますので操作としては簡単です。しかしその際に音質は変わってしまっているのです。
またこのことは、プロジェクトのサンプリング周波数をいくつにするのかを決定する際に重要になってきます。プロジェクトのサンプリング周波数は最初に決めます。途中で変えることはできません。もちろんサンプリング周波数が高い方が音質は良いのですがCPUの負荷が大きくなります。また最終的に出力するフォーマットに合わせないと最後の最後で劣化してしまう可能性があります。
最近はPCの処理能力が上がってきたため制作時のサンプリング周波数は96kHzでやる人が多いのですが、最終的に44.1kHzにすることを考えると、整数倍の88.2kHzの方が良い、という意見もあります。しかし使う元素材が88.1kHzであることはほとんどない(96kHzだったりする)ため最初の時点でコンバートが増える点や、リスニング環境で88.1kHzのオーディオファイルを扱えないことがあるため後々の素材確認が多少面倒である点、最も利用されている96kHz→44.1kHzのコンバートの品質が最近向上していることなどを考えると、あまり普及していない88.1kHzをあえて使うのはリスクの方が大きいのではないかと思います。
というわけで、PCの能力に余力があって良いオーディオインターフェイスを使っている人は96kHz、PCの能力に余裕がないかあるいはPC内蔵インターフェイスを使っている人、フリーソフトなどでなんとかしようとしている人は44.1kHzにしておくのが無難だと思います。
いずれにしても、ビット深度(Bit)が大きければ大きいほど音質にも作業効率にもメリットがあるのに対し、サンプリング周波数(Hz)は人間の耳の可聴域が進化しない以上、あまり高くてもコストパフォーマンス的にはメリットが少ないと言えます。
内部演算○ビットってやつは何?
先ほど、デジタルオーディオのミックスの原理については簡単に説明しましたが、先程はあえて波形に余裕があるものを使って解説しましたのでミックスしても問題ありませんでした。しかし、例えば4Bitの音同士であったとしても、4Bitいっぱいいっぱいになっている音同士をミックスすると、場合によっては以下のようになります。
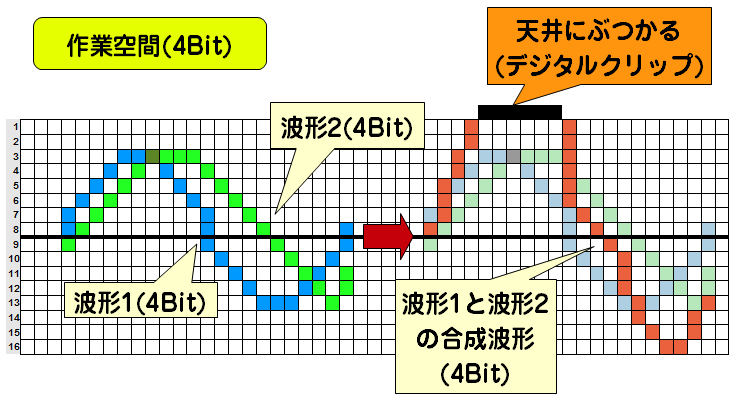
このように、単純足し算した結果、元のビット数に入りきれないことがあります。この足し算したら入り切れなくなった現象のことをデジタルクリップと言います。音楽編集では、いかにデジタルクリップしないように音楽を完成させるかが要です。しかしこれを回避するのはとても簡単です。例えば、元の波形が4Bitであっても編集している環境が5Bitであれば、このように問題なくなります。
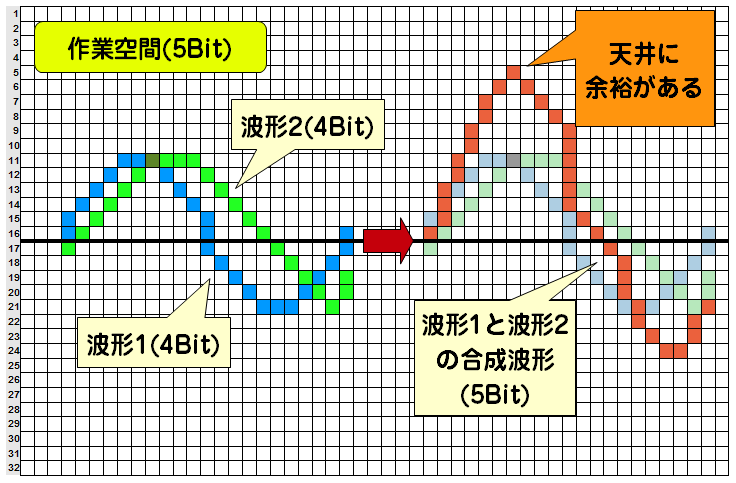
このように、編集している素材(音)のビット数にかかわらず、編集空間のビット数を大きめにとっておくことで、元の波形を壊さずにミックスすることができます。この編集空間のビット数が、よくDAWのスペック表などに書かれている内部演算○ビットです。
この内部演算のビット数は大きければ大きいほどミックス時には有利です。たとえば16Bitの音声を100トラック重ねた場合、偶然同じ場所で振り切っている波形があるとしたら、最大で16Bit(=65,536分割)の100倍の6,553,600の解像度が必要になります。この場合22Bit(=4,194,304)では足りませんが23Bit(=8,388,608)では十分となります。
この計算でいくと、元音+8Bitあれば128トラックまではクリップしない、ということになります。16Bit録音ならば24Bit、24Bit録音なら32Bitの内部演算精度があれば128トラックまでは十分、ということです。ただしこれは単純ミックスの場合で、トラックで元の音(0dB)よりもレベルを上げたりエフェクタなどを通したりするとこの限りではありません。なので、内部演算のビット数には余裕を持っておくに越したことはありません。ちなみにこの余裕のことをヘッドルームと呼びます。ヘッドルームというのはいろんな意味で使われている言葉ですが、ミックス時に「ヘッドルーム十分にあるから各トラックのレベルのことは気にしなくていいよ」という時のヘッドルームはこれのことです。
浮動小数(Float)って何?
さて、この辺から説明する方も読む方も面倒臭い内容になっていきます(笑)。
最近のDAWでは内部演算精度は32Bit(Float)か64Bit(Float)が主流です。このFloatっていうのは何だ?という話です。
Floatというのは浮動小数点のことです。ここまでに説明してきたクリップの話とかヘッドルームの話は、すべて固定小数点演算もしくは整数演算が前提の話で、浮動小数点演算というのはそれとはまた別のルールになっている、と覚えてください。それから、ややこしいことに32BitFloatの波形に使用できるビット深度は24Bitであるということも覚えてください。なぜかというと残りの8ビットを「浮動」のために使うからです。以後、Floatでない場合には(固定)と書きます。正確には固定小数点演算と整数演算があるのですが、話を簡略化するためこの両者をここでは「固定」としておきます。
これまでの説明では「24Bit(固定)録音で内部演算32Bit(固定)なら100トラックくらいならヘッドルーム足りてるよ」という話だったわけですが、それはつまり「24Bit(固定)録音で内部演算32Bit(Float)だと、24Bit(固定)相当なので100トラックもあるとヘッドルームが全然足りないよ」ということになるわけです。じゃあ32Bit(Float)よりも32Bit(固定)の方がいいじゃん、ということになりかねないわけですが、Floatにはものすごい特徴があって、こいつは「絶対にクリップしない」のです。なのでヘッドルームは気にしなくていいのです。つまり「24Bit(固定)録音で内部演算32Bit(Float)だと、24Bit(固定)相当なので100トラックもあるとヘッドルームが全然足りないんだけど、Floatなのでクリップしないよ」というわけです。
もう何の話だかわからない人もいるかもしれませんが、いつものように図を見てください。話を簡略化するために、実質24Bitのビット深度を持つ32Bit(Float)の変わりに、実質4Bitのビット深度を持つ8Bit(Float)というものがあると仮定して、これを4Bit(固定)と比較してみます。
まずは、それぞれの波形のレベルを下げて半分にしてみます。ちなみに、ここでいう半分というのはデータ上の半分であってフェーダーの位置を半分することとは意味が違います。
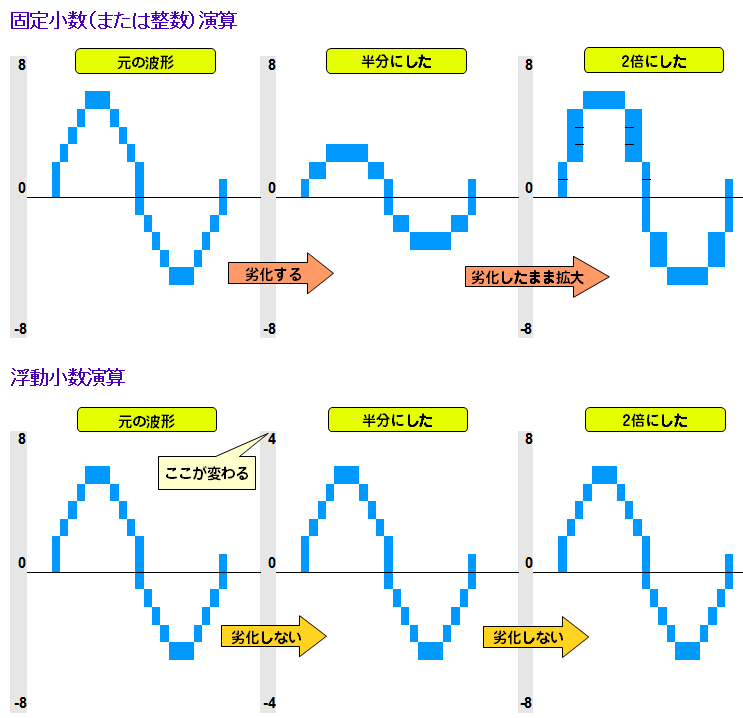
このように、レベルを半分にすると固定(ここでは整数)演算だと1Bit下がって音が劣化してしまいますが、Floatだと波形そのものは変わらずにマス目の値そのものが変わっています。固定とか浮動というのはこのように波形を描くために用意されているマス目側の目盛の数値が動く、ということです。
今度は逆にレベルを2倍にしてみます。
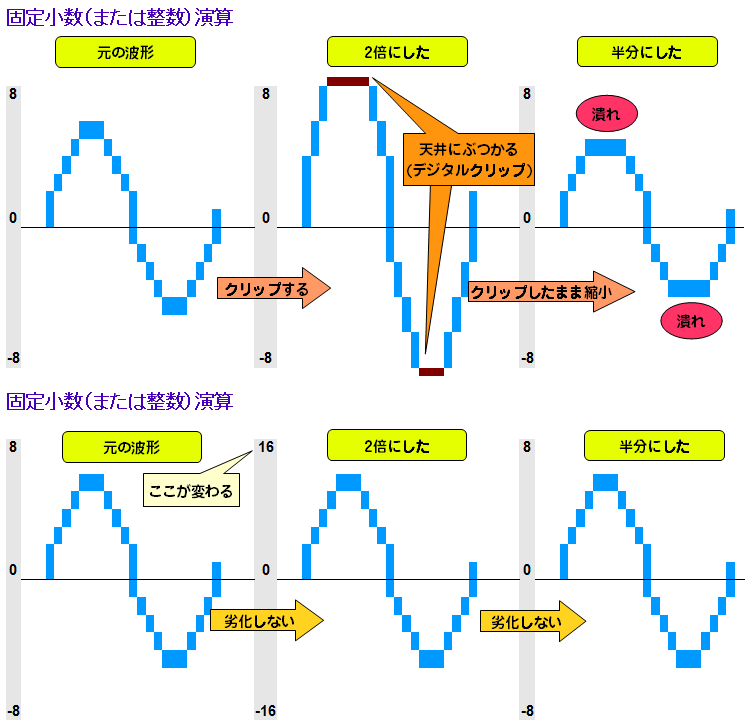
このようにレベル大きくした場合、固定演算だとクリップしてしまいますが、Floatだと目盛の数値が変わっただけです。これでFloatはクリップしない、の意味がおわかりいただけたでしょうか?
では、Floatは万能なのか? というとそんなことはありません。例えば小さい音と大きい音をミックスした場合、内部演算が固定の場合にはクリップしない限りどちらの情報も正確に保存されてミックスされますが、内部演算が浮動の場合にはクリップしないかわりに小さい方が適宜省略されていきます(丸め誤差)。また、内部演算が浮動の場合には解像度のわりに負荷が高い、例えば32Bit(Float)の場合、24Bit(固定)と比較すると解像度は同等であるにもかかわらずPCにはより大きな負荷を強いてしまいますし、32Bit(固定)と比較すると負荷は同等ながら解像度は落ちてしまいます。
それから64Bit(Float)について。前述のように32Bit(Float)は解像度が24Bitしかないので、素材が24Bitの場合には解像度が足りないこともあります。そこで最近のDAWでは内部演算64Bit(Float)のものも増えてきています。64Bit(Float)の解像度は53Bitです。11Bit分が「浮動」のために使われます。
なお、内部演算というのはDAW本体が演算を行なう時のもので、プラグインについてはそれぞれ独自の演算精度を持っています。「内部演算がFloatだからクリップしないと思ったのにクリップするじゃん」という問題はたいていプラグインが原因です。プラグインの内部演算やプラグインの出入口のレベルによってはクリップする可能性があるので注意が必要です。
サンプリング周波数と再生周波数の上限とアンチエイリアスについて
サンプリング周波数の解説のところで、サンプリング周波数は音の高さに影響する、と書きました。これはもちろんサンプリング周波数が高いと音が高い、という意味ではありません。そんなことになったら大変です(笑)
サンプリング周波数が高いと、高い音もちゃんと記録できる、ということです。では具体的にどのくらい高い音が記録されるんでしょうか? これは非常に簡単で、サンプリング周波数の半分の高さの音まで記録し再生することができます。たとえば44.1kHzの場合は22.05kHzが音の高さの上限です。
では、なぜサンプリング周波数そのものが上限でなく、サンプリング周波数の半分が上限なのでしょうか?
これについてはサ○レコなどに登場有名なレコーディングエンジニアさんですら以下のような間違ったことを書いていたりして目を疑います。
いやいや、違います(笑) それは原因と結果が逆です。ローパスフィルターを掛けてるから再生周波数の上限が半分なのではなくて、再生周波数上限がサンプリング周波数の半分だから半分の周波数でローパスフィルターを掛けているんですよ。
じゃあ何故、サンプリング周波数の半分が再生周波数の上限なのか。これはとても簡単な話で、エリアシングノイズとかローパスフィルタとかは一切関係ありません。
周波数(Hz)というのは1秒間に何個あるかを示す単位です。しかし音波とデジタル信号ではその1個数え方が違います。波形というのは上に行って戻って下に行って戻ってで1周期と数えます。それが1秒間に何周期あるかいうことです。一方で、サンプリング周波数は図でいうところの1マス目が1秒間にいくつあるかということになります。
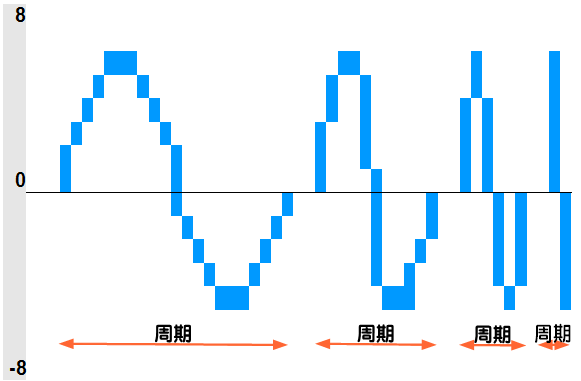
この図を見たらわかるでしょうか。波形の1周期を表現するためには最低でも上と下の最低2マス必要になります。それ以上の周波数になると波形として表現できません。だから、サンプリング周波数の半分が再生周波数の上限になるわけです。
なお、エリアシングノイズというのは、この論理上上限であるサンプリング周波数÷2以上の音が実際には出る現象のことを言います。これは、デジタル波形がなめらかでなくカクカクしているため不要な奇数倍音が出てしまうのが原因です(上限以上の音が出るのはいいことじゃないの?と思うかもしれませんが、論理的に正しい音ではないので残すメリットはありません)。なので、デジタル機器のD/Aコンバーターはこのエリアシングノイズを除去するために論理上の上限であるサンプリング周波数÷2でローパスフィルターを掛けそれ以上の周波数の音を除去します。この処理のことをアンチエリアス処理と言います。
ちなみに「どうせ聞こえないのであればローパスフィルターもいらないのでは?」という意見もあるかもしれません。実際音声以外の分野では技術が向上して解像度があまりに高くなるとエリアシングノイズを除去するためにローパスフィルターを付けることにあまり意味がなくなってくるというケースが出てきています。例えばデジカメの分野ではローパスレスが注目されています。音声の分野では今のところローパスフィルターは健在のようですが、これについては今後の研究を待ちましょう。
パソコンの○ビットCPUとかOSの○ビットってやつは?
ということで一通りの説明が終わったのですが、ここでかなりまぎらわしいもう一つのビットの話です。製品の名称やカタログなどのスペック表などで以下のようなものを見かけると思います。
OS : Windows 7 Professional 64Bit版
DAWソフト : SONAR X2 64Bit版
プラグイン音源 : KONTAKT 5 64Bit版
ここに出てくる「64Bit」というのは、ここまで話してきた64Bitとは基本的に何の関係もありません。これらはコンピュータが計算される際の演算ルールやメモリ管理ルールが64BitCPU用に最適化されているソフトウェア、という意味です。
現在のPC用(Macを含む)のCPUのほとんどはAMD64あるいはその互換品で、旧世代のx86という 32Bit CPU との上位互換性を持つ 64Bit CPU です。上位互換性を持つというのは、64Bit CPU 上で32Bitのソフトウェアを動かすことができる、という意味です。
一応互換関係を記しておきますと、64Bit CPUを搭載したパソコンではWindowsの32Bit版をインストールすることもできますし64Bit版をインストールすることもできます。もし64Bit版Windowsをインストールした場合、その上に64Bitソフト(DAWなど)をインストールすることもできますし、32Bit版ソフトをインストールすることもできます。32Bit版Windows上に64Bit版のソフトウェアをインストールすることはできません。もし64Bit版のDAWをインストールした場合、64Bit版のプラグインだけを使用することができ、32Bit版のDAWをインストールした場合には32Bit版のプラグインだけを使用することができます。ただし、ブリッジを使用すると64Bit版のDAW上で32Bit版のプラグインを使用することができます。逆に32Bit版のDAWの場合にはブリッジを使用しても64Bit版のDAWを使用することはできません。
で、これを本題のオーディオの内部演算処理の話を掛け合せてみるとどうなるでしょう? 32Bit版のDAWの内部演算は何Bitでしょうか?64Bit版は?32Bit版のプラグインの内部演算は?
これらは、実はケースバイケースです。32Bit版のDAWでも内部演算は64Bit(Float)かもしれませんし64BitのDAWでも内部演算は32Bit(Float)かもしれません。また、名称に64を冠した「PX-64」のようなプラグインもありますが、この64の意味は内部演算の話ですので、32Bit版のPX-64というものも存在します。
というわけで、OSはCPUが32Bitであろうと64Bitであろうと、内部演算が何Bitなのかには関係ありませんので、音質にも影響はありません(ただし同時使用プラグイン数などの性能には影響しますので作品の出来上がりには関係する場合もあるでしょう)。
というわけで…
長いテキストをお読みいただきありがとうございました。
いろいろ書きましたが、誤解の多いポイントだけおさらいすると
・OSやソフトが32Bitでも内部演算64BitのDAWやプラグインは使えるよ。
・32Bit(Float)の解像度は24Bitしかないよ。
・再生限界周波数はローパスフィルタで決まるわけじゃないよ。
と言ったところでしょうか。
次回は制作模様に戻りたいと思います。そろそろコーラスについて書こうと思います。
では。
※この記事中に技術的な誤りや、誤植などのご指摘があればコメントまたはツイッター@tmkw1までお願いします。なお、波形のグリッドで0のところにごまかしがある点は解説をシンプルにするためにあえてそうしています。
